geographical convergent cross mapping

Usage

# S4 method for class 'sf'
gccm(
  data,
  cause,
  effect,
  libsizes = NULL,
  E = 3,
  k = E + 2,
  tau = 1,
  style = 1,
  stack = FALSE,
  lib = NULL,
  pred = NULL,
  dist.metric = "L2",
  dist.average = TRUE,
  theta = 1,
  algorithm = "simplex",
  threads = detectThreads(),
  detrend = TRUE,
  parallel.level = "low",
  bidirectional = TRUE,
  progressbar = TRUE,
  nb = NULL
)

# S4 method for class 'SpatRaster'
gccm(
  data,
  cause,
  effect,
  libsizes = NULL,
  E = 3,
  k = E + 2,
  tau = 1,
  style = 1,
  stack = FALSE,
  lib = NULL,
  pred = NULL,
  dist.metric = "L2",
  dist.average = TRUE,
  theta = 1,
  algorithm = "simplex",
  threads = detectThreads(),
  detrend = TRUE,
  parallel.level = "low",
  bidirectional = TRUE,
  progressbar = TRUE,
  grid.coord = TRUE,
  embed.direction = 0,
  win.ratio = 0
)

Arguments

data: observation data.
cause: name of causal variable.
effect: name of effect variable.
libsizes: (optional) number of spatial units used.
E: (optional) embedding dimensions.
k: (optional) number of nearest neighbors.
tau: (optional) step of spatial lags.
style: (optional) embedding style (0 includes current state, 1 excludes it).
stack: (optional) whether to stack embeddings.
lib: (optional) libraries indices.
pred: (optional) predictions indices.
dist.metric: (optional) distance metric (L1: Manhattan, L2: Euclidean).
dist.average: (optional) whether to average distance.
theta: (optional) weighting parameter for distances, useful when algorithm is smap.
algorithm: (optional) prediction algorithm.
threads: (optional) number of threads to use.
detrend: (optional) whether to remove the linear trend.
parallel.level: (optional) level of parallelism, low or high.
bidirectional: (optional) whether to examine bidirectional causality.
progressbar: (optional) whether to show the progress bar.
nb: (optional) neighbours list.
grid.coord: (optional) whether to detrend using cell center coordinates (TRUE) or row/column numbers (FALSE).
embed.direction: (optional) direction selector for embeddings (0 returns all directions, 1-8 correspond to NW, N, NE, W, E, SW, S, SE).
win.ratio: (optional) ratio of sliding window scale to speed up state-space predictions.

Value

A list

xmap: cross mapping results
varname: names of causal and effect variable
bidirectional: whether to examine bidirectional causality

References

Gao, B., Yang, J., Chen, Z. et al. Causal inference from cross-sectional earth system data with geographical convergent cross mapping. Nat Commun 14, 5875 (2023).

Examples

columbus = sf::read_sf(system.file("case/columbus.gpkg", package="spEDM"))
# \donttest{
g = gccm(columbus,"hoval","crime",libsizes = seq(5,45,5),E = 6)
#> 
Computing: [========================================] 100% (done)                         
#> 
Computing: [========================================] 100% (done)                         
g
#>   libsizes hoval->crime crime->hoval
#> 1        5    0.1253050    0.2568469
#> 2       10    0.1762769    0.3961522
#> 3       15    0.2197481    0.4672470
#> 4       20    0.2324435    0.5144297
#> 5       25    0.2354728    0.5713321
#> 6       30    0.2360934    0.6048914
#> 7       35    0.2412944    0.6253026
#> 8       40    0.2383788    0.6364897
#> 9       45    0.2339483    0.6484721
plot(g, ylimits = c(0,0.85))

# }
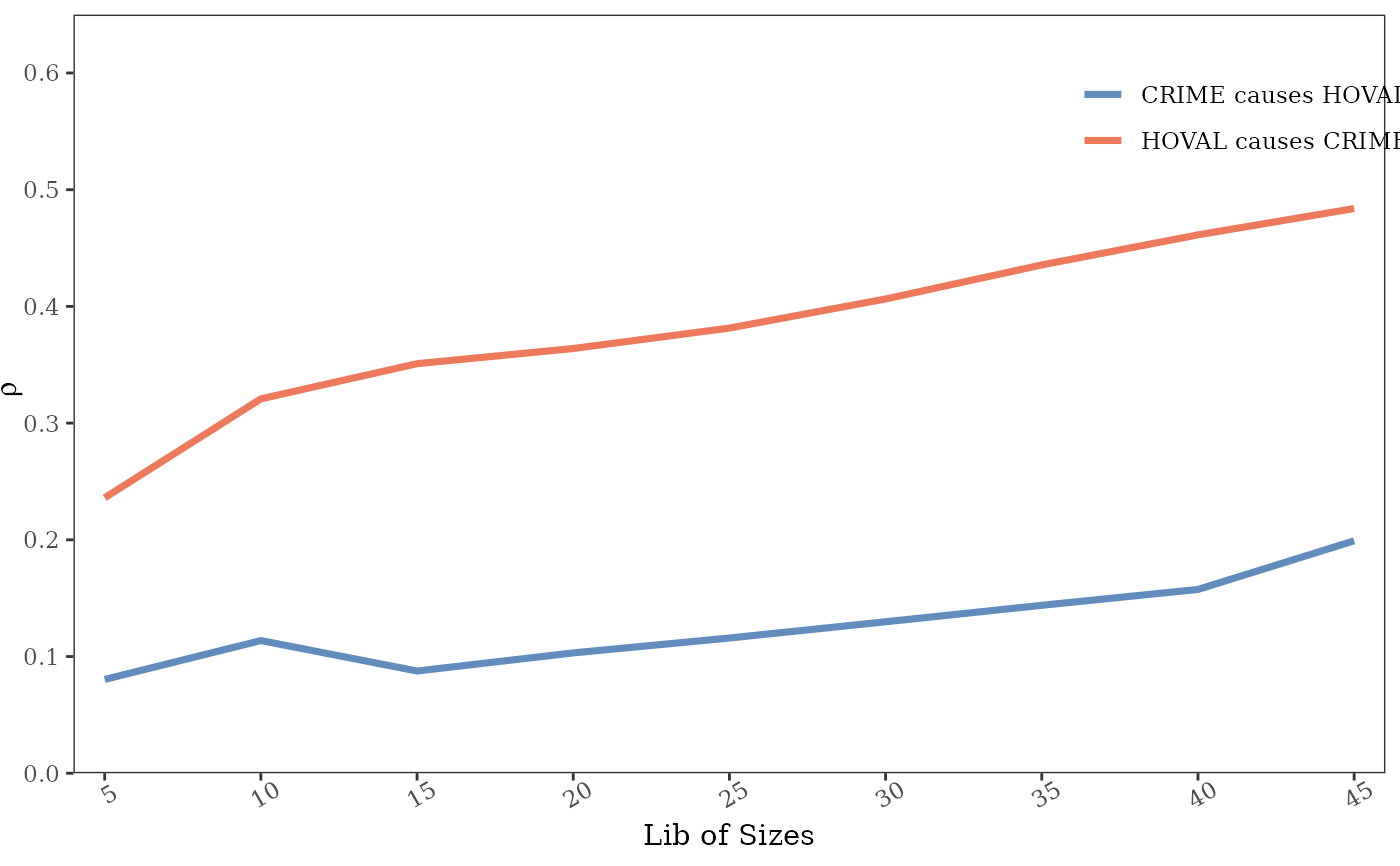