Geographical Convergent Cross Mapping (GCCM)
Wenbo Lv
2025-05-01
Source:vignettes/GCCM.Rmd
GCCM.RmdModel principles
Let \(Y = \{y_i\}\) and \(X = \{x_i\}\) be the two spatial cross sectional variable, where \(i = 1, 2, \dots, n\) denotes spatial units (e.g., regions or grid cells), the shadow manifolds of \(X\) can be constructed using the different spatial lag values of all spatial units:
\[ M_{x} = \begin{bmatrix} S_{(1)}(x_1) & S_{(1 + \tau)}(x_1) & \cdots & S_{(1+(E-1)\tau)}(x_1) \\ S_{(1)}(x_2) & S_{(1 + \tau)}(x_2) & \cdots & S_{(1+(E-1)\tau)}(x_2) \\ \vdots & \vdots & \ddots & \vdots \\ S_{(1)}(x_n) & S_{(1 + \tau)}(x_n) & \cdots & S_{(1+(E-1)\tau)}(x_n) \end{bmatrix} \]
Here, \(S_{(j)}(x_i)\) denotes the \(j\) th-order spatial lag value of spatial unit \(i\), $$ is the step size for the spatial lag order, and \(E\) is the embedding dimension and \(M_{x}\) corresponds to the shadow manifolds of \(X\).
With the reconstructed shadow manifolds \(M_{x}\), the state of Y can be predicted with the state of X through
\[ \hat{Y}_s \mid M_x = \sum\limits_{i=1}^k \left(\omega_{si}Y_{si} \mid M_x \right) \]
where \(s\) represents a spatial unit at which the value of \(Y\) needs to be predicted, \(\hat{Y}_s\) is the prediction result, \(k\) is the number of nearest neighbors used for prediction, \(si\) is the spatial unit used in the prediction, \(Y_{si}\) is the observation value of \(Y\) at \(si\). \(\omega_{si}\) is the corresponding weight defined as:
\[ \omega_{si} \mid M_x = \frac{weight \left(\psi\left(M_x,s_i\right),\psi\left(M_x,s\right)\right)}{\sum_{i=1}^{L+1}weight \left(\psi\left(M_x,s_i\right),\psi\left(M_x,s\right)\right)} \]
where \(\psi(M_x, s_i)\) is the state vector of spatial unit \(s_i\) in the shadow manifold $ M_x$, and \(weight (\ast, \ast)\) is the weight function between two states in the shadow manifold, defined as:
\[ weight \left(\psi\left(M_x,s_i\right),\psi\left(M_x,s\right)\right) = \exp \left(- \frac{dis \left(\psi\left(M_x,s_i\right),\psi\left(M_x,s\right)\right)}{dis \left(\psi\left(M_x,s_1\right),\psi\left(M_x,s\right)\right)} \right) \]
where \(\exp\) is the exponential function and \(dis \left(\ast,\ast\right)\) represents the distance function between two states in the shadow manifold defined as:
\[ dis \left( \psi(M_x, s_i), \psi(M_x, s) \right) = \frac{1}{E} \sum_{m=1}^{E} \left| \psi_m(M_x, s_i) - \psi_m(M_x, s) \right| \]
where \(dis \left( \psi(M_x, s_i), \psi(M_x, s) \right)\) denotes the average absolute difference between corresponding elements of the two state vectors in the shadow manifold \(M_x\), \(E\) is the embedding dimension, and \(\psi_m(M_x, s_i)\) is the \(m\)-th element of the state vector \(\psi(M_x, s_i)\).
The skill of cross-mapping prediction \(\rho\) is measured by the Pearson correlation coefficient between the true observations and corresponding predictions, and the confidence interval of \(\rho\) can be estimated based the \(z\)-statistics with the normal distribution:
\[ \rho = \frac{Cov\left(Y,\hat{Y}\mid M_x\right)}{\sqrt{Var\left(Y\right) Var\left(\hat{Y}\mid M_x\right)}} \]
\[ t = \rho \sqrt{\frac{n-2}{1-\rho^2}} \]
where \(n\) is the number of observations to be predicted, and
\[ z = \frac{1}{2} \ln \left(\frac{1+\rho}{1-\rho}\right) \]
The prediction skill \(\rho\) varies by setting different sizes of libraries, which means the quantity of observations used in reconstruction of the shadow manifold. We can use the convergence of \(\rho\) to infer the causal associations. For GCCM, the convergence means that \(\rho\) increases with the size of libraries and is statistically significant when the library becomes largest.
\[ \rho_{x \to y} = \lim_{L \to \infty} cor \left( Y,\hat{Y}\mid M_x \right) \]
where \(\rho_{x \to y}\) is the correlation after convergence, used to measure the causation effect from \(Y\) to \(X\), despite the notation suggesting the reverse direction.
Usage examples
An example of spatial lattice data
Load the spEDM package and its county-level population
density data:
library(spEDM)
popd_nb = spdep::read.gal(system.file("case/popd_nb.gal",package = "spEDM"))
## Warning in spdep::read.gal(system.file("case/popd_nb.gal", package = "spEDM")):
## neighbour object has 4 sub-graphs
popd = readr::read_csv(system.file("case/popd.csv",package = "spEDM"))
## Rows: 2806 Columns: 7
## ── Column specification ────────────────────────────────────────────────────────────────────────────
## Delimiter: ","
## dbl (7): x, y, popd, elev, tem, pre, slope
##
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.
popd_sf = sf::st_as_sf(popd, coords = c("x","y"), crs = 4326)
popd_sf
## Simple feature collection with 2806 features and 5 fields
## Geometry type: POINT
## Dimension: XY
## Bounding box: xmin: 74.9055 ymin: 18.2698 xmax: 134.269 ymax: 52.9346
## Geodetic CRS: WGS 84
## # A tibble: 2,806 × 6
## popd elev tem pre slope geometry
## * <dbl> <dbl> <dbl> <dbl> <dbl> <POINT [°]>
## 1 780. 8 17.4 1528. 0.452 (116.912 30.4879)
## 2 395. 48 17.2 1487. 0.842 (116.755 30.5877)
## 3 261. 49 16.0 1456. 3.56 (116.541 30.7548)
## 4 258. 23 17.4 1555. 0.932 (116.241 30.104)
## 5 211. 101 16.3 1494. 3.34 (116.173 30.495)
## 6 386. 10 16.6 1382. 1.65 (116.935 30.9839)
## 7 350. 23 17.5 1569. 0.346 (116.677 30.2412)
## 8 470. 22 17.1 1493. 1.88 (117.066 30.6514)
## 9 1226. 11 17.4 1526. 0.208 (117.171 30.5558)
## 10 137. 598 13.9 1458. 5.92 (116.208 30.8983)
## # ℹ 2,796 more rowsSelect the appropriate embedding dimension E:
simplex(popd_sf,"pre",lib = 1:2000,pred = 2001:nrow(popd_sf),k = 6,nb = popd_nb,trend.rm = TRUE)
## The suggested E and k for variable pre is 2 and 6
simplex(popd_sf,"popd",lib = 1:2000,pred = 2001:nrow(popd_sf),k = 6,nb = popd_nb,trend.rm = TRUE)
## The suggested E and k for variable popd is 5 and 6We choose the E with the highest rho and the lowest MAE and RMSE as
the most suitable one. Under the selected lib and pred, the optimal
embedding dimension E for the variable pre is 2, and for
the variable popdensity, it is 5.
Then, run GCCM:
startTime = Sys.time()
pd_res = gccm(data = popd_sf,
cause = "pre",
effect = "popd",
libsizes = seq(10, 2800, by = 100),
E = c(2,5),
k = 6,
nb = popd_nb,
progressbar = FALSE)
endTime = Sys.time()
print(difftime(endTime,startTime, units ="mins"))
## Time difference of 5.971936 mins
pd_res
## libsizes pre->popd popd->pre
## 1 10 0.05589905 0.01004636
## 2 110 0.18109636 0.03478543
## 3 210 0.24325566 0.04932428
## 4 310 0.27657692 0.06417637
## 5 410 0.30630281 0.07634983
## 6 510 0.34116169 0.08815848
## 7 610 0.38078810 0.09890353
## 8 710 0.41612716 0.10867846
## 9 810 0.44420437 0.11714337
## 10 910 0.46815429 0.12485229
## 11 1010 0.48876449 0.13194552
## 12 1110 0.50538462 0.13802611
## 13 1210 0.52300459 0.14335037
## 14 1310 0.53902632 0.14813342
## 15 1410 0.55309048 0.15284706
## 16 1510 0.56754023 0.15777314
## 17 1610 0.58387624 0.16301596
## 18 1710 0.60029184 0.16768202
## 19 1810 0.61631190 0.17202960
## 20 1910 0.63213899 0.17601166
## 21 2010 0.64785899 0.17979878
## 22 2110 0.66289302 0.18304365
## 23 2210 0.67740971 0.18596497
## 24 2310 0.69156193 0.18906187
## 25 2410 0.70541793 0.19196548
## 26 2510 0.71925253 0.19503355
## 27 2610 0.73287448 0.19819076
## 28 2710 0.74435871 0.20116518Visualize the result:
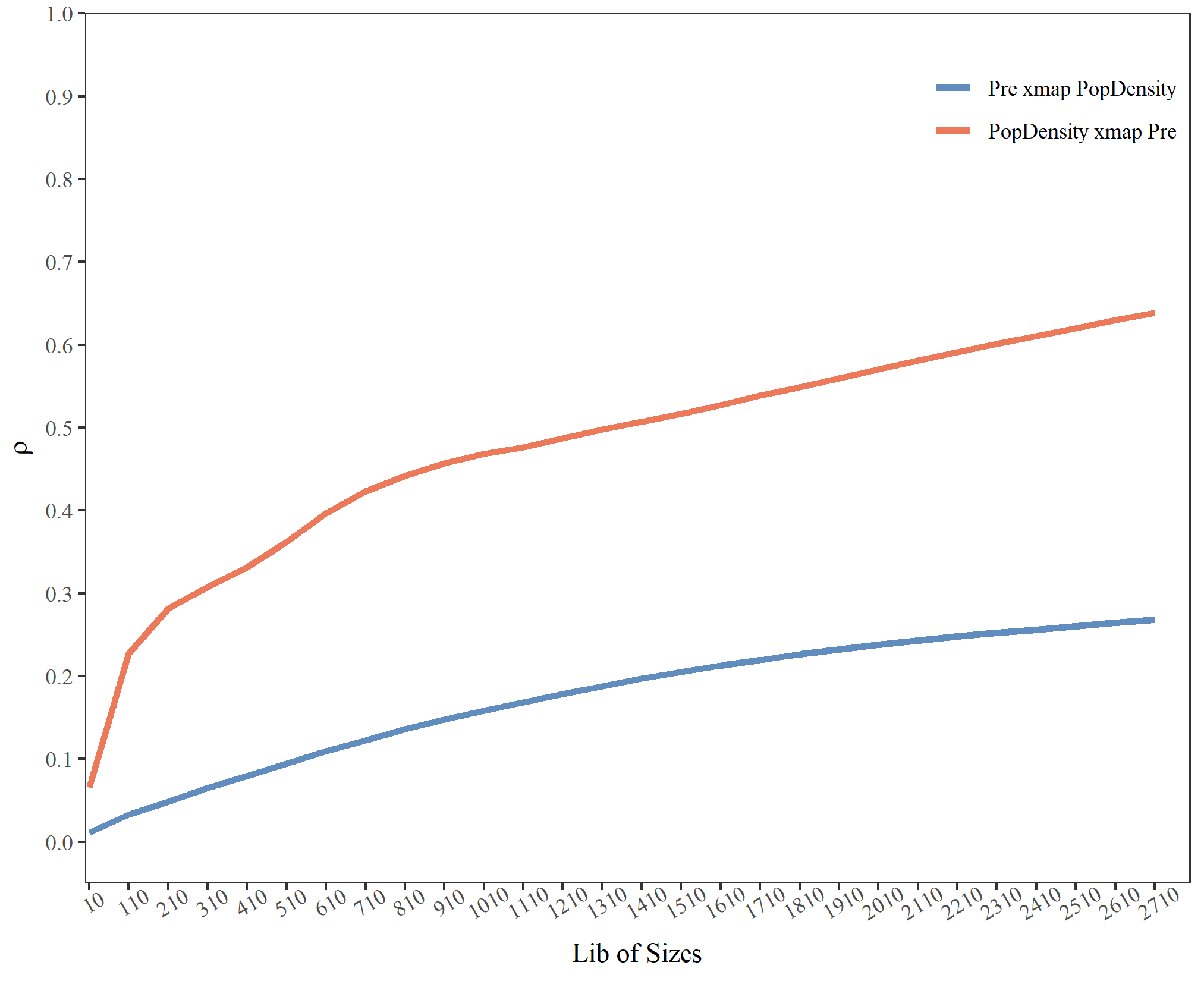
An example of spatial grid data
Load the spEDM package and its farmland NPP data:
library(spEDM)
npp = terra::rast(system.file("case/npp.tif", package = "spEDM"))
npp
## class : SpatRaster
## dimensions : 404, 483, 4 (nrow, ncol, nlyr)
## resolution : 10000, 10000 (x, y)
## extent : -2625763, 2204237, 1877078, 5917078 (xmin, xmax, ymin, ymax)
## coord. ref. : CGCS2000_Albers
## source : npp.tif
## names : npp, pre, tem, elev
## min values : 164.00, 384.3409, -47.8194, -122.2004
## max values : 16606.33, 23878.3555, 263.6938, 5350.4902
# To save the computation time, we will aggregate the data by 3 times
npp = terra::aggregate(npp, fact = 3, na.rm = TRUE)
npp
## class : SpatRaster
## dimensions : 135, 161, 4 (nrow, ncol, nlyr)
## resolution : 30000, 30000 (x, y)
## extent : -2625763, 2204237, 1867078, 5917078 (xmin, xmax, ymin, ymax)
## coord. ref. : CGCS2000_Albers
## source(s) : memory
## names : npp, pre, tem, elev
## min values : 187.50, 390.3351, -47.8194, -110.1494
## max values : 15381.89, 23734.5330, 262.8576, 5217.6431
# Inspect NA values
terra::global(npp,"isNA")
## isNA
## npp 14815
## pre 14766
## tem 14766
## elev 14760
terra::ncell(npp)
## [1] 21735
nnamat = terra::as.matrix(npp[[1]], wide = TRUE)
nnaindice = which(!is.na(nnamat), arr.ind = TRUE)
dim(nnaindice)
## [1] 6920 2
# Select 1500 non-NA pixels to predict:
set.seed(2025)
indices = sample(nrow(nnaindice), size = 1500, replace = FALSE)
libindice = nnaindice[-indices,]
predindice = nnaindice[indices,]Due to the high number of NA values in the npp raster data, we used all non-NA cell as the libraries when testing for the most suitable embedding dimensions.
simplex(npp,"pre",nnaindice,predindice,k = 8,trend.rm = TRUE)
## The suggested E and k for variable pre is 2 and 8
simplex(npp,"npp",nnaindice,predindice,k = 8,trend.rm = TRUE)
## The suggested E and k for variable npp is 10 and 8Under the selected lib and pred, the optimal embedding dimension E
for the variable pre is 2, and for the variable
npp, it is 10.
Then, run GCCM:
startTime = Sys.time()
npp_res = gccm(data = npp,
cause = "pre",
effect = "npp",
libsizes = as.matrix(expand.grid(seq(10,130,10),seq(10,160,10))),
E = c(2,10),
k = 8,
lib = nnaindice,
pred = predindice,
progressbar = FALSE)
endTime = Sys.time()
print(difftime(endTime,startTime, units ="mins"))
## Time difference of 9.60704 mins
npp_res
## libsizes pre->npp npp->pre
## 1 10 0.1295281 0.1013898
## 2 20 0.1990710 0.1605447
## 3 30 0.2607783 0.2286559
## 4 40 0.3219650 0.2744616
## 5 50 0.3788341 0.2956426
## 6 60 0.4512668 0.3272331
## 7 70 0.4961658 0.3394660
## 8 80 0.5366037 0.3378108
## 9 90 0.5972341 0.3376894
## 10 100 0.6670024 0.3405838
## 11 110 0.7358447 0.3412305
## 12 120 0.7981711 0.3500295
## 13 130 0.8386849 0.3663077
## 14 140 0.8460446 0.3687385
## 15 150 0.8483344 0.3696080
## 16 160 0.8503816 0.3695784Visualize the result:
plot(npp_res,xlimits = c(9, 161),ylimits = c(0.05,1)) +
ggplot2::theme(legend.justification = c(0.25,1))