Geographical Pattern Causality
Wenbo Lv
Last
update: 2025-11-15
Last run: 2025-11-15
Source: Last run: 2025-11-15
vignettes/GPC.Rmd
GPC.RmdMethodological Background
Geographical Pattern Causality (GPC) infers causal relations from spatial cross-sectional data by reconstructing a symbolic approximation of the underlying spatial dynamical system.
Let \(x(s)\) and \(y(s)\) denote two spatial cross-sections over locations \(s \in \mathcal{S}\).
(1) Spatial Embedding
For each location \(s_i\), GPC constructs an embedding vector
\[ \mathbf{E}_{x(s_i)} = \big( x(s_{i}^{(1)}), x(s_{i}^{(2)}), \dots, x(s_{i}^{(E\tau)}) \big), \]
where \(s_{i}^{(k)}\) denotes the \(k\)-th spatially lagged value of the spatial unit \(s_i\), determined by embedding dimension \(E\) and lag \(\tau\). This yields two reconstructed state spaces \(\mathcal{M}_x, \mathcal{M}_y \subset \mathbb{R}^E\).
(2) Symbolic Pattern Extraction
Local geometric transitions in each manifold are mapped to symbols
\[ \sigma_x(s_i),; \sigma_y(s_i) \in \mathcal{A}, \]
encoding increasing, decreasing, or non-changing modes. These symbolic trajectories summarize local pattern evolution.
(3) Cross-Pattern Mapping
Causality from \(x \to y\) is assessed by predicting:
\[ \hat{\sigma}_y(s_i) = F\big( \sigma_x(s_j): s_j \in \mathcal{N}_k(s_i) \big), \]
where \(\mathcal{N}_k\) denotes the set of \(k\) nearest neighbors in \(\mathcal{M}_x\). The agreement structure between \(\hat{\sigma}_y(s_i)\) and \(\sigma_y(s_i)\) determines the causal mode:
- Positive: \(\hat{\sigma}_y = \sigma_y\)
- Negative: \(\hat{\sigma}_y = -\sigma_y\)
- Dark: neither agreement nor opposition
(4) Causal Strength
The global causal strength is the normalized consistency of symbol matches:
\[ C_{x \to y} = \frac{1}{|\mathcal{S}|} \sum_{s_i \in \mathcal{S}} \mathbb{I}\big[ \hat{\sigma}_y(s_i) \bowtie \sigma_y(s_i) \big], \]
where \(\bowtie\) encodes positive, negative, or dark matching rules.
Usage examples
An example of spatial lattice data
Load the spEDM package and its columbus spatial analysis
data:
library(spEDM)
columbus = sf::read_sf(system.file("case/columbus.gpkg", package="spEDM"))
columbus
## Simple feature collection with 49 features and 6 fields
## Geometry type: POLYGON
## Dimension: XY
## Bounding box: xmin: 5.874907 ymin: 10.78863 xmax: 11.28742 ymax: 14.74245
## Projected CRS: Undefined Cartesian SRS with unknown unit
## # A tibble: 49 × 7
## hoval inc crime open plumb discbd geom
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <POLYGON>
## 1 80.5 19.5 15.7 2.85 0.217 5.03 ((8.624129 14.23698, 8.5597 14.74245, …
## 2 44.6 21.2 18.8 5.30 0.321 4.27 ((8.25279 14.23694, 8.282758 14.22994,…
## 3 26.4 16.0 30.6 4.53 0.374 3.89 ((8.653305 14.00809, 8.81814 14.00205,…
## 4 33.2 4.48 32.4 0.394 1.19 3.7 ((8.459499 13.82035, 8.473408 13.83227…
## 5 23.2 11.3 50.7 0.406 0.625 2.83 ((8.685274 13.63952, 8.677577 13.72221…
## 6 28.8 16.0 26.1 0.563 0.254 3.78 ((9.401384 13.5504, 9.434411 13.69427,…
## 7 75 8.44 0.178 0 2.40 2.74 ((8.037741 13.60752, 8.062716 13.60452…
## 8 37.1 11.3 38.4 3.48 2.74 2.89 ((8.247527 13.58651, 8.2795 13.5965, 8…
## 9 52.6 17.6 30.5 0.527 0.891 3.17 ((9.333297 13.27242, 9.671007 13.27361…
## 10 96.4 13.6 34.0 1.55 0.558 4.33 ((10.08251 13.03377, 10.0925 13.05275,…
## # ℹ 39 more rowsThe false nearest neighbours (FNN) method helps identify the appropriate minimal embedding dimension for reconstructing the state space of a time series or spatial cross-sectional data.
spEDM::fnn(columbus, "crime", E = 1:10, eps = stats::sd(columbus$crime))
## E:1 E:2 E:3 E:4 E:5 E:6 E:7
## 0.59183673 0.04081633 0.04081633 0.10204082 0.00000000 0.00000000 0.00000000
## E:8
## 0.00000000The false nearest neighbours (FNN) ratio decreased to approximately 0.001 when the embedding dimension E reached 7, and remained relatively stable thereafter. Therefore, we adopted \(E = 7\) as the minimal embedding dimension for subsequent parameter search.
Then, search optimal parameters:
spEDM::pc(columbus, "hoval", "crime", E = 5:10, k = 6:12)
## The suggested E,k,tau for variable crime is 5, 6 and 1Run geographical pattern causality analysis
spEDM::gpc(columbus, "hoval", "crime", E = 5, k = 6)
## --------------------------------
## ***pattern causality analysis***
## --------------------------------
## type strength direction
## 1 positive NaN hoval -> crime
## 2 negative NaN hoval -> crime
## 3 dark 0.2780607 hoval -> crime
## 4 positive NaN crime -> hoval
## 5 negative 0.8347013 crime -> hoval
## 6 dark 0.2665406 crime -> hovalConvergence diagnostics
crime_convergence = spEDM::gpc(columbus, "hoval", "crime",
libsizes = seq(5, 45, by = 5),
E = 5, k = 6, progressbar = FALSE)
crime_convergence
## --------------------------------
## ***pattern causality analysis***
## --------------------------------
## libsizes type mean q05 q50 q95 direction
## 1 10 positive 0.00000000 0.00000000 0.000000000 0.0000000 hoval -> crime
## 2 15 positive 0.00000000 0.00000000 0.000000000 0.0000000 hoval -> crime
## 3 20 positive 0.00000000 0.00000000 0.000000000 0.0000000 hoval -> crime
## 4 25 positive 0.00000000 0.00000000 0.000000000 0.0000000 hoval -> crime
## 5 30 positive 0.00000000 0.00000000 0.000000000 0.0000000 hoval -> crime
## 6 35 positive 0.00000000 0.00000000 0.000000000 0.0000000 hoval -> crime
## 7 40 positive 0.00000000 0.00000000 0.000000000 0.0000000 hoval -> crime
## 8 45 positive 0.00000000 0.00000000 0.000000000 0.0000000 hoval -> crime
## 9 10 negative 0.06197905 0.00000000 0.000000000 0.2122731 hoval -> crime
## 10 15 negative 0.09733382 0.00000000 0.008436065 0.3764162 hoval -> crime
## 11 20 negative 0.16973789 0.00000000 0.079063725 0.6827156 hoval -> crime
## 12 25 negative 0.19585505 0.00000000 0.163092046 0.7090052 hoval -> crime
## 13 30 negative 0.21620032 0.00000000 0.184693649 0.6105418 hoval -> crime
## 14 35 negative 0.27419530 0.00000000 0.291693414 0.6387668 hoval -> crime
## 15 40 negative 0.29505999 0.00000000 0.301567205 0.6858029 hoval -> crime
## 16 45 negative 0.28582637 0.00000000 0.278714857 0.7823519 hoval -> crime
## 17 10 dark 0.06909548 0.01466280 0.064407248 0.1306970 hoval -> crime
## 18 15 dark 0.09379292 0.03032706 0.090038526 0.1753795 hoval -> crime
## 19 20 dark 0.10990907 0.05273241 0.111527731 0.1812541 hoval -> crime
## 20 25 dark 0.13626822 0.07348148 0.132795897 0.2066249 hoval -> crime
## 21 30 dark 0.16691561 0.10837075 0.164160188 0.2323193 hoval -> crime
## 22 35 dark 0.20811342 0.14493342 0.205565119 0.2830248 hoval -> crime
## 23 40 dark 0.23123661 0.16032023 0.231884982 0.3024902 hoval -> crime
## 24 45 dark 0.25667436 0.19059340 0.262871437 0.3119186 hoval -> crime
## 25 10 positive 0.00000000 0.00000000 0.000000000 0.0000000 crime -> hoval
## 26 15 positive 0.00000000 0.00000000 0.000000000 0.0000000 crime -> hoval
## 27 20 positive 0.00000000 0.00000000 0.000000000 0.0000000 crime -> hoval
## 28 25 positive 0.00000000 0.00000000 0.000000000 0.0000000 crime -> hoval
## 29 30 positive 0.00000000 0.00000000 0.000000000 0.0000000 crime -> hoval
## 30 35 positive 0.00000000 0.00000000 0.000000000 0.0000000 crime -> hoval
## 31 40 positive 0.00000000 0.00000000 0.000000000 0.0000000 crime -> hoval
## 32 45 positive 0.00000000 0.00000000 0.000000000 0.0000000 crime -> hoval
## 33 10 negative 0.09654436 0.00000000 0.000000000 0.3586954 crime -> hoval
## 34 15 negative 0.20393585 0.00000000 0.209139006 0.7079035 crime -> hoval
## 35 20 negative 0.32201217 0.00000000 0.354644641 0.7737565 crime -> hoval
## 36 25 negative 0.42664655 0.00000000 0.387706242 0.8178587 crime -> hoval
## 37 30 negative 0.57588175 0.22782805 0.732695557 0.8347013 crime -> hoval
## 38 35 negative 0.64433710 0.27861320 0.789691315 0.8347013 crime -> hoval
## 39 40 negative 0.68771823 0.40682155 0.810940395 0.8359320 crime -> hoval
## 40 45 negative 0.80291152 0.41832745 0.834701302 0.8368720 crime -> hoval
## 41 10 dark 0.12603205 0.04863464 0.120620434 0.2110495 crime -> hoval
## 42 15 dark 0.14482113 0.07541432 0.138866743 0.2314505 crime -> hoval
## 43 20 dark 0.16382185 0.08162589 0.161596344 0.2379369 crime -> hoval
## 44 25 dark 0.17266178 0.11528366 0.174319496 0.2334413 crime -> hoval
## 45 30 dark 0.19812654 0.13584290 0.200169607 0.2599632 crime -> hoval
## 46 35 dark 0.22141279 0.15870776 0.221354140 0.2861718 crime -> hoval
## 47 40 dark 0.24194166 0.18537228 0.243766935 0.2914456 crime -> hoval
## 48 45 dark 0.25798204 0.21830835 0.259892742 0.2999078 crime -> hoval
plot(crime_convergence, ylimits = c(-0.01,1),
xlimits = c(9,46), xbreaks = seq(10, 45, 10))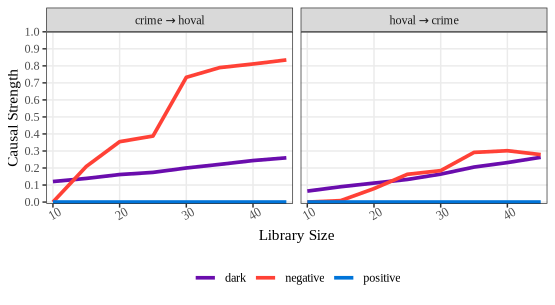
Figure 1. Convergence
curves of causal strengths among house value and crime.
An example of spatial grid data
Load the spEDM package and its farmland NPP data:
library(spEDM)
npp = terra::rast(system.file("case/npp.tif", package = "spEDM"))
# To save the computation time, we will aggregate the data by 3 times
npp = terra::aggregate(npp, fact = 3, na.rm = TRUE)
npp
## class : SpatRaster
## size : 135, 161, 5 (nrow, ncol, nlyr)
## resolution : 30000, 30000 (x, y)
## extent : -2625763, 2204237, 1867078, 5917078 (xmin, xmax, ymin, ymax)
## coord. ref. : CGCS2000_Albers
## source(s) : memory
## names : npp, pre, tem, elev, hfp
## min values : 187.50, 390.3351, -47.8194, -110.1494, 0.04434316
## max values : 15381.89, 23734.5330, 262.8576, 5217.6431, 42.68803711
# Check the validated cell number
nnamat = terra::as.matrix(npp[[1]], wide = TRUE)
nnaindice = which(!is.na(nnamat), arr.ind = TRUE)
dim(nnaindice)
## [1] 6920 2Determining minimal embedding dimension:
fnn(npp, "npp", E = 1:15,
eps = stats::sd(terra::values(npp[["npp"]]),na.rm = TRUE))
## E:1 E:2 E:3 E:4 E:5 E:6
## 0.9813070569 0.5309427415 0.1322254335 0.0167630058 0.0017341040 0.0000000000
## E:7 E:8 E:9 E:10 E:11 E:12
## 0.0001445087 0.0000000000 0.0000000000 0.0000000000 0.0002890173 0.0000000000
## E:13 E:14
## 0.0001445087 0.0001445087At \(E = 6\), the false nearest neighbor ratio stabilizes approximately at 0.0001 and remains constant thereafter. Therefore, \(E = 6\) is selected as minimal embedding dimension for the subsequent GPC analysis.
Then, search optimal parameters:
g1 = spEDM::pc(npp, "npp", "pre", E = 6:10, k = 7:12)
g1
## The suggested E,k,tau for variable pre is 10, 8 and 1Run geographical pattern causality analysis
spEDM::gpc(npp, "pre", "npp", E = 10, k = 8)
## --------------------------------
## ***pattern causality analysis***
## --------------------------------
## type strength direction
## 1 positive 0.17965602 pre -> npp
## 2 negative 0.07729251 pre -> npp
## 3 dark 0.11239454 pre -> npp
## 4 positive 0.10920578 npp -> pre
## 5 negative 0.01839649 npp -> pre
## 6 dark 0.07731815 npp -> preConvergence diagnostics
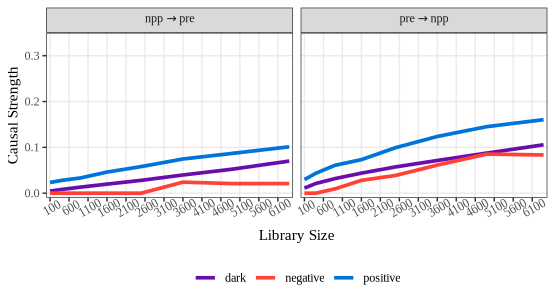
npp_convergence = spEDM::gpc(npp, "pre", "npp",
libsizes = matrix(rep(seq(10,80,10),2),ncol = 2),
E = 10, k = 8, progressbar = FALSE)
npp_convergence
## --------------------------------
## ***pattern causality analysis***
## --------------------------------
## libsizes type mean q05 q50 q95 direction
## 1 100 positive 0.031115313 0.007586101 0.029699586 0.058335871 pre -> npp
## 2 400 positive 0.046321136 0.025965817 0.043444827 0.072677663 pre -> npp
## 3 900 positive 0.061289327 0.036546196 0.060742103 0.088607440 pre -> npp
## 4 1600 positive 0.076140862 0.052179914 0.073213997 0.109569849 pre -> npp
## 5 2500 positive 0.099999344 0.061554432 0.099303348 0.138071568 pre -> npp
## 6 3600 positive 0.126697417 0.098448170 0.123791233 0.167912560 pre -> npp
## 7 4900 positive 0.146035271 0.112762146 0.145172371 0.183307027 pre -> npp
## 8 6400 positive 0.160439882 0.134164256 0.160445471 0.186289425 pre -> npp
## 9 100 negative 0.005034612 0.000000000 0.000000000 0.040091076 pre -> npp
## 10 400 negative 0.009928927 0.000000000 0.000000000 0.052005414 pre -> npp
## 11 900 negative 0.019165255 0.000000000 0.009337993 0.059256988 pre -> npp
## 12 1600 negative 0.029471659 0.000000000 0.027997599 0.073358489 pre -> npp
## 13 2500 negative 0.045285442 0.000000000 0.038739984 0.117191230 pre -> npp
## 14 3600 negative 0.065880615 0.018235836 0.061356270 0.141681812 pre -> npp
## 15 4900 negative 0.084468586 0.022971353 0.085285422 0.147335973 pre -> npp
## 16 6400 negative 0.084044451 0.049760990 0.083386491 0.119344985 pre -> npp
## 17 100 dark 0.011013023 0.007197887 0.011167831 0.015515615 pre -> npp
## 18 400 dark 0.020940904 0.017941858 0.021144785 0.024073808 pre -> npp
## 19 900 dark 0.031601592 0.028162694 0.031760585 0.035366888 pre -> npp
## 20 1600 dark 0.043908454 0.040426567 0.043749224 0.047899451 pre -> npp
## 21 2500 dark 0.057340747 0.053427426 0.057373516 0.060924723 pre -> npp
## 22 3600 dark 0.071494236 0.068717216 0.071382799 0.074614915 pre -> npp
## 23 4900 dark 0.087452806 0.084720124 0.087498875 0.090183299 pre -> npp
## 24 6400 dark 0.105697810 0.103544775 0.105670612 0.108333330 pre -> npp
## 25 100 positive 0.030463575 0.006797979 0.023451241 0.072539552 npp -> pre
## 26 400 positive 0.032101886 0.010252731 0.027835285 0.064829814 npp -> pre
## 27 900 positive 0.035869465 0.014164942 0.033232723 0.067018898 npp -> pre
## 28 1600 positive 0.049411311 0.020915010 0.046109502 0.085792572 npp -> pre
## 29 2500 positive 0.061779406 0.030886961 0.058038123 0.104777473 npp -> pre
## 30 3600 positive 0.076992050 0.043158420 0.074651929 0.126986637 npp -> pre
## 31 4900 positive 0.086996180 0.054796887 0.086869797 0.120530012 npp -> pre
## 32 6400 positive 0.101064523 0.078249392 0.101266631 0.131261057 npp -> pre
## 33 100 negative 0.001047740 0.000000000 0.000000000 0.000000000 npp -> pre
## 34 400 negative 0.003933528 0.000000000 0.000000000 0.030443193 npp -> pre
## 35 900 negative 0.007788536 0.000000000 0.000000000 0.051665613 npp -> pre
## 36 1600 negative 0.015474525 0.000000000 0.000000000 0.073222926 npp -> pre
## 37 2500 negative 0.033992370 0.000000000 0.000000000 0.138902382 npp -> pre
## 38 3600 negative 0.035942024 0.000000000 0.024083469 0.122359197 npp -> pre
## 39 4900 negative 0.021465683 0.000000000 0.020887613 0.054454265 npp -> pre
## 40 6400 negative 0.024594728 0.000000000 0.021011738 0.048068745 npp -> pre
## 41 100 dark 0.004628748 0.003073966 0.004491904 0.006746096 npp -> pre
## 42 400 dark 0.008084206 0.006384447 0.008101869 0.009793286 npp -> pre
## 43 900 dark 0.013248915 0.011023435 0.013180761 0.015348453 npp -> pre
## 44 1600 dark 0.019759343 0.016800507 0.019801600 0.022120016 npp -> pre
## 45 2500 dark 0.028182746 0.025560203 0.028047957 0.030789268 npp -> pre
## 46 3600 dark 0.039660053 0.036114552 0.039729568 0.042630349 npp -> pre
## 47 4900 dark 0.052345674 0.048603242 0.052403669 0.055987952 npp -> pre
## 48 6400 dark 0.069830135 0.067058436 0.070112629 0.072162472 npp -> pre
plot(npp_convergence, ylimits = c(-0.01,0.35),
xlimits = c(0,6500), xbreaks = seq(100, 6400, 500))
Figure 2. Convergence
curves of causal strengths among precipitation and NPP.