Spatially Convergent Partial Cross Mapping
Wenbo Lv
Last
update: 2026-01-23
Last run: 2026-01-23
Source: Last run: 2026-01-23
vignettes/main6_scpcm.Rmd
main6_scpcm.RmdModel principles
The methodological details are pending peer review and will be made available thereafter.
Usage examples
Example of spatial vector data
Load the spEDM package and columbus OH spatial analysis
dataset:
if (!requireNamespace("spEDM")) install.packages("spEDM")
## Loading required namespace: spEDM
columbus = sf::read_sf(system.file("case/columbus.gpkg", package="spEDM"))
columbus
## Simple feature collection with 49 features and 6 fields
## Geometry type: POLYGON
## Dimension: XY
## Bounding box: xmin: 5.874907 ymin: 10.78863 xmax: 11.28742 ymax: 14.74245
## Projected CRS: Undefined Cartesian SRS with unknown unit
## # A tibble: 49 × 7
## hoval inc crime open plumb discbd geom
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <POLYGON>
## 1 80.5 19.5 15.7 2.85 0.217 5.03 ((8.624129 14.23698, 8.5597 14.74245, 8…
## 2 44.6 21.2 18.8 5.30 0.321 4.27 ((8.25279 14.23694, 8.282758 14.22994, …
## 3 26.4 16.0 30.6 4.53 0.374 3.89 ((8.653305 14.00809, 8.81814 14.00205, …
## 4 33.2 4.48 32.4 0.394 1.19 3.7 ((8.459499 13.82035, 8.473408 13.83227,…
## 5 23.2 11.3 50.7 0.406 0.625 2.83 ((8.685274 13.63952, 8.677577 13.72221,…
## 6 28.8 16.0 26.1 0.563 0.254 3.78 ((9.401384 13.5504, 9.434411 13.69427, …
## 7 75 8.44 0.178 0 2.40 2.74 ((8.037741 13.60752, 8.062716 13.60452,…
## 8 37.1 11.3 38.4 3.48 2.74 2.89 ((8.247527 13.58651, 8.2795 13.5965, 8.…
## 9 52.6 17.6 30.5 0.527 0.891 3.17 ((9.333297 13.27242, 9.671007 13.27361,…
## 10 96.4 13.6 34.0 1.55 0.558 4.33 ((10.08251 13.03377, 10.0925 13.05275, …
## # ℹ 39 more rowsWe demonstrate how spatial vector data can be used in SCPCM analysis through a causal example examining the influences of the level of burglary incidents in a neighbourhood on house values, with neighbourhood household income included as a conditioning variable.
Determine minimum embedding dimensions:
spEDM::fnn(columbus,"crime",E = 1:10)
## E:1 E:2 E:3 E:4 E:5 E:6 E:7
## 0.79591837 0.53061224 0.63265306 0.51020408 0.12244898 0.04081633 0.00000000
## E:8
## 0.00000000
spEDM::fnn(columbus,"hoval",E = 1:10)
## E:1 E:2 E:3 E:4 E:5 E:6 E:7
## 0.85714286 0.77551020 0.51020408 0.61224490 0.22448980 0.08163265 0.00000000
## E:8
## 0.00000000
spEDM::fnn(columbus,"inc",E = 1:10)
## E:1 E:2 E:3 E:4 E:5 E:6 E:7
## 0.73469388 0.24489796 0.30612245 0.38775510 0.24489796 0.04081633 0.00000000
## E:8
## 0.00000000Self prediction for parameter turning:
spEDM::simplex(columbus,"crime","crime",E = 7:10,k=12)
## The suggested E,k,tau for variable crime is 8, 12 and 1
spEDM::simplex(columbus,"hoval","hoval",E = 7:10,k=12)
## The suggested E,k,tau for variable hoval is 7, 12 and 1
spEDM::simplex(columbus,"inc","inc",E = 7:10,k=12)
## The suggested E,k,tau for variable inc is 8, 12 and 1Conduct SCPCM:
crime_hoval = spEDM::scpcm(data = columbus,
cause = "crime",
effect = "hoval",
conds = "inc",
libsizes = seq(5, 45, by = 5),
E = c(8,7,8),
k = 12,
progressbar = FALSE)
crime_hoval
## --------------------------------------
## ***partial cross mapping prediction***
## --------------------------------------
## libsizes crime->hoval hoval->crime
## 1 5 0.08948688 0.022401607
## 2 10 0.14511673 0.062986079
## 3 15 0.16849249 0.080653365
## 4 20 0.20940427 0.040974217
## 5 25 0.23160147 0.026613757
## 6 30 0.24709326 0.001942294
## 7 35 0.29707812 -0.014879976
## 8 40 0.33591810 -0.028758126
## 9 45 0.36337200 -0.040204136
##
## ------------------------------
## ***cross mapping prediction***
## ------------------------------
## libsizes crime->hoval hoval->crime
## 1 5 0.2224861 0.1378071
## 2 10 0.3023880 0.1880328
## 3 15 0.4005255 0.2085278
## 4 20 0.4681692 0.2203727
## 5 25 0.5098130 0.2293076
## 6 30 0.5467173 0.2326005
## 7 35 0.5732757 0.2331852
## 8 40 0.5822545 0.2361204
## 9 45 0.5883504 0.2364234Visualize the result:
if (!requireNamespace("cowplot")) install.packages("cowplot")
## Loading required namespace: cowplot
fig1a = plot(crime_hoval,partial = FALSE,ylimits = c(0.1,0.75))
fig1b = plot(crime_hoval,partial = TRUE,ylimits = c(-0.05,0.55))
fig1 = cowplot::plot_grid(fig1a,fig1b,ncol = 2,label_fontfamily = 'serif',
labels = paste0('(',letters[1:2],')'))
fig1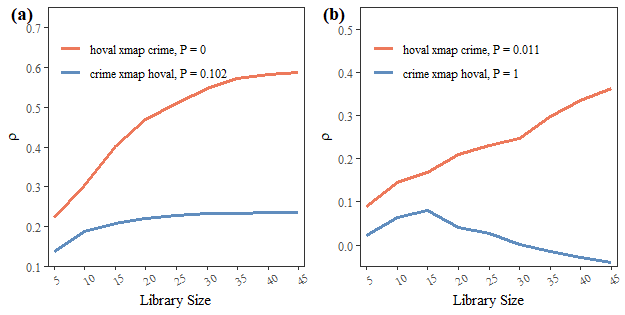
Figure 1. The cross mapping
between crime and house value. a Crime–hoval causality
without accounting for covariates. b Crime–hoval
causality controlling for household income.
Example of spatial raster data
Load the spEDM package and simulate raster data with a
cyclic interaction structure \(x \rightarrow y
\rightarrow z \rightarrow x\):
if (!requireNamespace("fields")) install.packages("fields")
## Loading required namespace: fields
if (!requireNamespace("MASS")) install.packages("MASS")
sim_trispecies = \(nx,ny,seed = 123){
grid = expand.grid(seq(0, 10, length.out = nx),
seq(0, 10, length.out = ny))
cov.fun = \(d, range = 1.5, sill=1) sill * exp(-d/range)
dist.mat = fields::rdist(grid)
cov.mat = cov.fun(dist.mat, range=1.5, sill=1)
set.seed(seed)
res = replicate(3, {
MASS::mvrnorm(1, rep(0, nrow(grid)), cov.mat) |>
pmax(0) |>
sdsfun::normalize_vector(0,1) |>
matrix(nrow = nx, ncol = ny) |>
terra::rast()
}, simplify = FALSE)
terra::rast(res)
}
species = sim_trispecies(20,20, seed = 42)
names(species) = c("x","y","z")
sim = spEDM::slm(species, x = "x", y = "y", z = "z", k = 4,
step = 15, transient = 1, threshold = Inf,
aggregate_fn = \(.x) mean(.x, na.rm = TRUE),
alpha_x = 0.05, alpha_y = 0.05, alpha_z = 0.05,
beta_xy = 1, beta_xz = 0, beta_yx = 0, beta_yz = 1,
beta_zx = 1, beta_zy = 0)
terra::values(species[["x"]]) = sim$x
terra::values(species[["y"]]) = sim$y
terra::values(species[["z"]]) = sim$z
species
## class : SpatRaster
## size : 20, 20, 3 (nrow, ncol, nlyr)
## resolution : 1, 1 (x, y)
## extent : 0, 20, 0, 20 (xmin, xmax, ymin, ymax)
## coord. ref. :
## source(s) : memory
## names : x, y, z
## min values : 0.9984091, 0.9983558, 0.998285
## max values : 1.0009110, 1.0011445, 1.001050Determine minimum embedding dimensions:
spEDM::fnn(species, "x")
## E:1 E:2 E:3 E:4 E:5 E:6 E:7 E:8
## 0.8937824 0.3125000 0.0100000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
## E:9
## 0.0000000
spEDM::fnn(species, "y")
## E:1 E:2 E:3 E:4 E:5 E:6 E:7 E:8
## 0.9333333 0.2525000 0.0425000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
## E:9
## 0.0000000
spEDM::fnn(species, "z")
## E:1 E:2 E:3 E:4 E:5 E:6 E:7 E:8
## 0.9238845 0.3375000 0.0625000 0.0200000 0.0000000 0.0000000 0.0000000 0.0000000
## E:9
## 0.0000000Self prediction for parameter turning:
s1 = spEDM::simplex(species, "x", "x", E = 5:10, k = 15, tau = 1)
s2 = spEDM::simplex(species, "y", "y", E = 5:10, k = 15, tau = 1)
s3 = spEDM::simplex(species, "z", "z", E = 5:10, k = 15, tau = 1)
list(s1,s2,s3)
## [[1]]
## The suggested E,k,tau for variable x is 7, 15 and 1
##
## [[2]]
## The suggested E,k,tau for variable y is 9, 15 and 1
##
## [[3]]
## The suggested E,k,tau for variable z is 5, 15 and 1Due to the statistical aggregation performed after simulating with the spatial logistic map, we adopt a uniform embedding dimension for x, y, and z to reduce inference bias:
if (!requireNamespace("purrr")) install.packages("purrr")
## Loading required namespace: purrr
simplex_res = purrr::map2_dfr(list(s1,s2,s3), c("x","y","z"),
\(.list,.name) dplyr::mutate(.list$xmap,variable = .name))
ggplot2::ggplot(data = simplex_res) +
ggplot2::geom_line(ggplot2::aes(x = E, y = rho, color = variable)) +
ggplot2::theme_classic()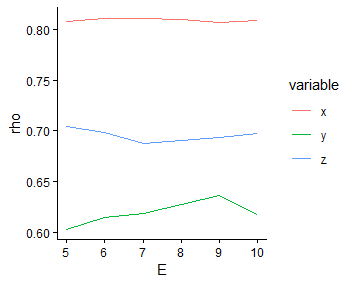
Figure 2. Self cross prediction
skills for three variables.
Since the self-prediction performance of the y variable is relatively weaker than that of x and z, we select the embedding dimension that yields the strongest predictive performance for y as the final dimension, that is \(E = 9\).
Investigate the causation between x and z, with y as control variables:
xz = spEDM::scpcm(species, "x", "z", "y", E = 9, k = 15,
libsizes = matrix(seq(50,400,50), ncol = 1),
progressbar = FALSE)
xz
## --------------------------------------
## ***partial cross mapping prediction***
## --------------------------------------
## libsizes x->z z->x
## 1 50 0.07977338 0.1020714
## 2 100 0.10473775 0.1762694
## 3 150 0.14175015 0.1959109
## 4 200 0.20562278 0.2543825
## 5 250 0.25500417 0.3300376
## 6 300 0.27904324 0.3956866
## 7 350 0.31249554 0.4597477
## 8 400 0.28091955 0.4843444
##
## ------------------------------
## ***cross mapping prediction***
## ------------------------------
## libsizes x->z z->x
## 1 50 0.1542880 0.1368370
## 2 100 0.1827606 0.2217753
## 3 150 0.2426258 0.2781118
## 4 200 0.3239733 0.3487456
## 5 250 0.4035323 0.4185710
## 6 300 0.4653763 0.4835619
## 7 350 0.5190529 0.5553776
## 8 400 0.5658039 0.5938894Visualize the result:
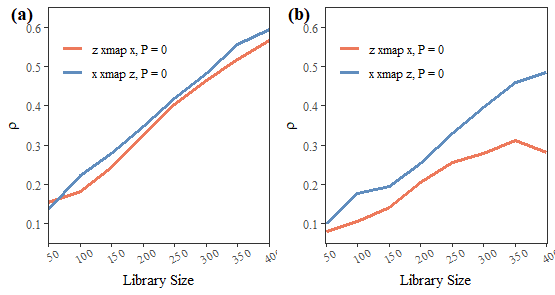
fig2a = plot(xz,partial = FALSE,ylimits = c(0.05,0.65))
fig2b = plot(xz,partial = TRUE,ylimits = c(0.05,0.65))
fig2 = cowplot::plot_grid(fig2a,fig2b,ncol = 2,label_fontfamily = 'serif',
labels = paste0('(',letters[1:2],')'))
fig2
Figure 3. The cross mapping
between x and z. a x–z causality without accounting for
y. b x–z causality controlling for y.